Az utóbbi bő tíz évben harmadszor ért el rekordmagasságot a Duna Budapesten. A 2002-es és 2006-os csúcsmagasságot 2013-ban ismét megdöntötte a folyó. Ezt kiegészíthetjük még azzal is, hogy a képzeletbeli toplista ötödik helyén a 2010-es év található, és a 2000-es évek utáni legmagasabb vízszintek mellett csak 1965 került be a lista negyedik helyére.
Vajon mekkora volt annak a valószínűsége, hogy 2002 és 2006 után ismét rekord magasságú vízállás lesz a Dunán? A választ a statisztika egy speciális ága adhatja meg számunkra, amely extrémérték eloszlásokkal foglalkozik. Ha a vízállások várható értékei köré szeretnénk konfidencia intervallumot szerkeszteni, nincs nehéz dolgunk, a statisztikát tanuló egyetemisták általában már az első év után meg tudnak oldani egy ilyen feladatot. A maximumok esetén azonban kicsit nehezebb a helyzet, mivel speciális eloszlásokat kell használni, ráadásul az idősor elemzéseknek külön eszköztára van a statisztikában. A tiszai árvizek kapcsán már készült hasonló elemzés (http://www.ksh.hu/statszemle_archive/2005/2005_10-11/2005_10-11_919.pdf), ennek analógiájára mutatom be a dunai árvizek előfordulásának valószínűségét. A budapesti adatokat a Központi Hidrológiai Adattárból gyűjtöttem le (http://www.hydroinfo.hu/vituki/archivum/), ahol Budapest vízállásáról 1876-tól minden egyes napra elérhető adat. Első lépésben minden évre kiszámítottam a budapesti vízállás maximumát. Ezt szemlélteti a következő ábra:
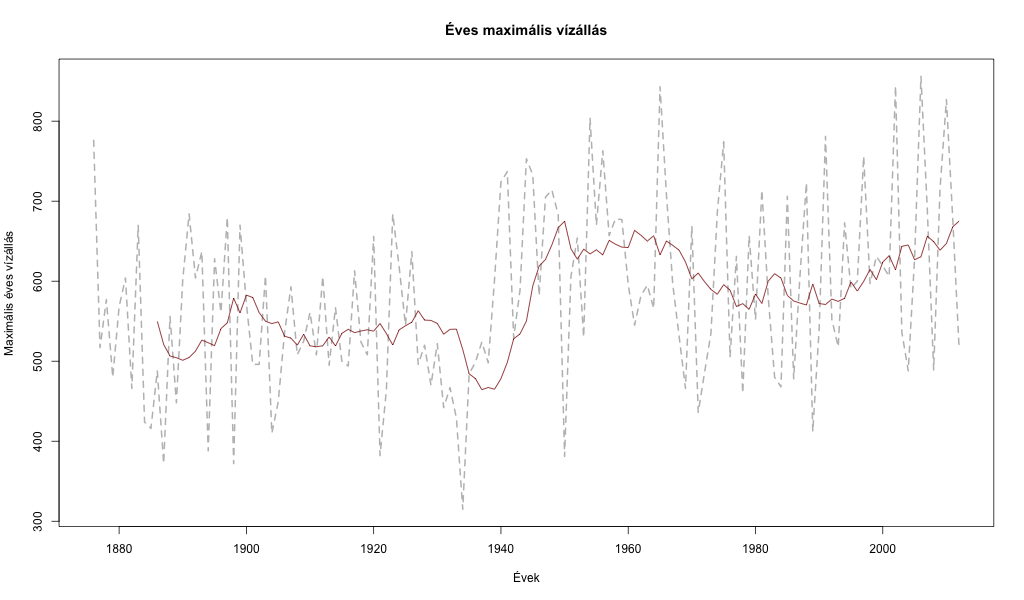
Ahogy látható, az idősor kilengése viszonylag nagy. A vastag piros vonal a tíz éves mozgó átlag simított értékét mutatja: ez alapján ugyan láthatóak rövid távú trendek (például egy enyhe felfelé irányuló trend megfigyelhető az 1990-es évek után), de az idősor alapvetően a maximum átlagához próbál visszatérni. Az átlaghoz való visszatértést erősíti az is, hogy a maximumokra kiszámolt hurst exponens értéke 0,15-ös értéket vesz fel (http://en.wikipedia.org/wiki/Hurst_exponent).
A maximum értékekre egy speciális eloszlást lehet illeszteni, amit a szakirodalomban általánosított extrémérték eloszlásnak (GEV) neveznek. Az eloszláshoz maximum likelihood módszerrel konfidencia intervallumot is lehet szerkeszteni, aminek segítségével jól modellezhető, hogy egy adott vízállás milyen gyakorisággal fordulhat elő újra. A modell egyik előfeltétele, hogy az idősorban szereplő egymást követő elemek függetlenek legyenek, valamint az, hogy az idősor stacionárius legyen (ne legyen benne trend- és ciklushatás). Az első előfeltételt többek között egy ARIMA modellel lehet tesztelni, amely alapján nincs autoregressziv folyamat az árvizek éves maximumában, tehát az adott év legmagasabb vízállása nem függ az előző év legmagasabb vízállásától. A stacionaritásra még visszatértünk, de előbb bemutatom azt a modellt, ami abból az előfeltevésből indul ki, hogy az idősor stacioner.
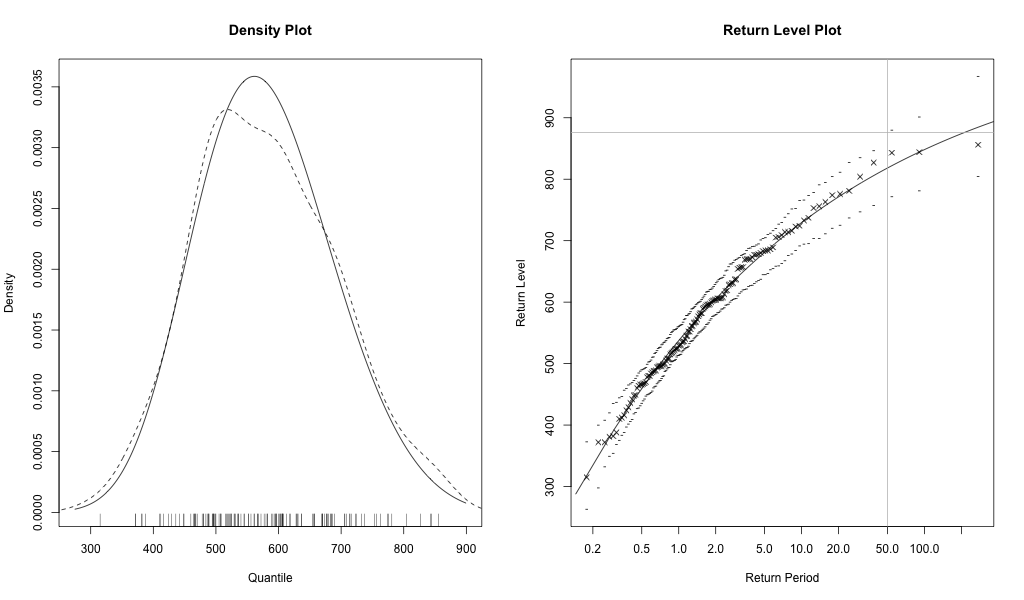
A baloldali ábra mutatja az elméleti és az empirikus eloszlást. Jól látható, hogy a maximumok átlagához közeli értékek az elméletileg vártnál ritkábban, míg extrém nagy és extrém kicsi értékek a vártnál valamennyivel nagyobb arányban fordultak elő. Ettől függetlenül a további statisztikák azt mutatták, hogy az elméleti eloszlás jól illeszkedett a vizsgált idősorra.
A jobboldali ábra mutatja az igazi érdekességet, a visszatérési szinteket. Az y tengelyen szürke vízszintes vonallal jelöltem a 2013-as árvíz szintet, és egy vertikális vonallal azt, hogy ez hol metszi a felső konfidencia intervallumot: eszerint ilyen nagyságú árvíz 99 százalékos valószínűség mellett maximálisan 50 évente fordulhatna elő. Ha ehhez hozzátesszük, hogy 2002-ben és 2006-ban is hasonló nagyságú vízállást mértek Budapesten, akkor egyértelműen kirajzolódik az, hogy a mostani árvíznek a valószínűsége extrém alacsony volt.
Ahogy korábban is utaltunk rá, egy enyhe emelkedő trend hatás figyelhető meg a vízállások maximumában. Ha az adatokra egy egyszerű lineáris trendvonalat illesztünk, akkor éves szinten megközelítőleg 0,8 centiméteres növekedés figyelhető meg az adatsorban. Ezt a trendet a modellből levonva újra elemeztem az idősort.
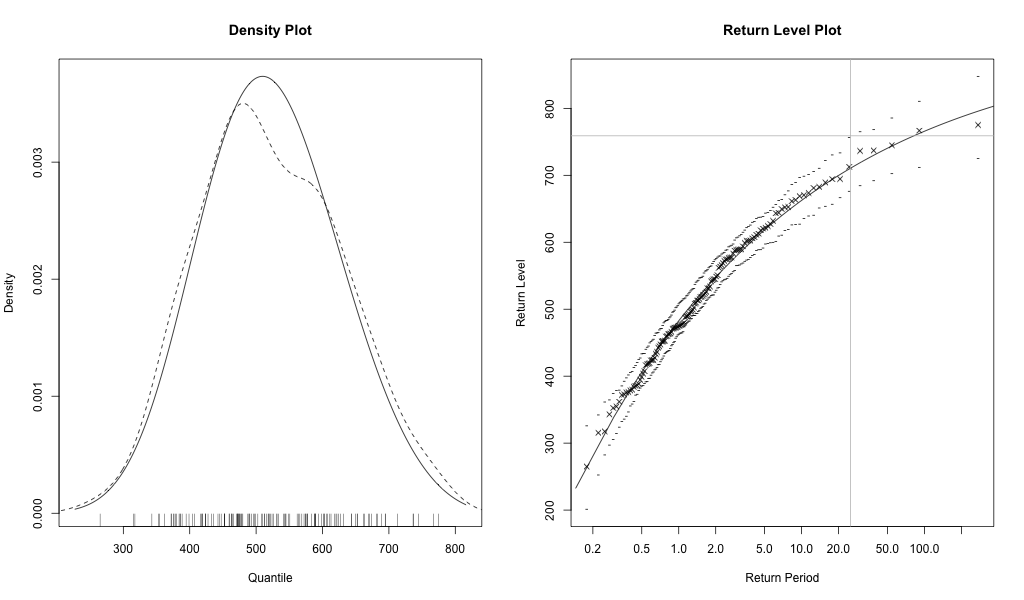
A jobboldali ábráról látható, hogy a trendet levonva a 2013-as árvíz már nem is a legmagasabb, és a visszatérés nagyjából 25 éves periódusra esett vissza, ami jóval kisebb, mint az elsőként számított 50 év, azonban továbbra sem oldja fel azt a problémát, hogy az utóbbi bő 10 évből 4 évben extrém magas volt a vízállás.
A megoldás kulcsa ilyen esetben abban keresendő, hogy a vízállási maximumok mögött lévő idősor generáló-mechanizmusa megváltozott. Hogy ennek a globális felmelegedés az oka, vagy a folyók szabályozásának megváltozása, esetleg bármi más, nem témája ennek az elemzésnek.
Ha az 1990 utáni adatokra illesztjük az elméleti eloszlást, akkor látható, hogy az extrém magas árvizek bekövetkezésének valószínűsége jelentős megnő.
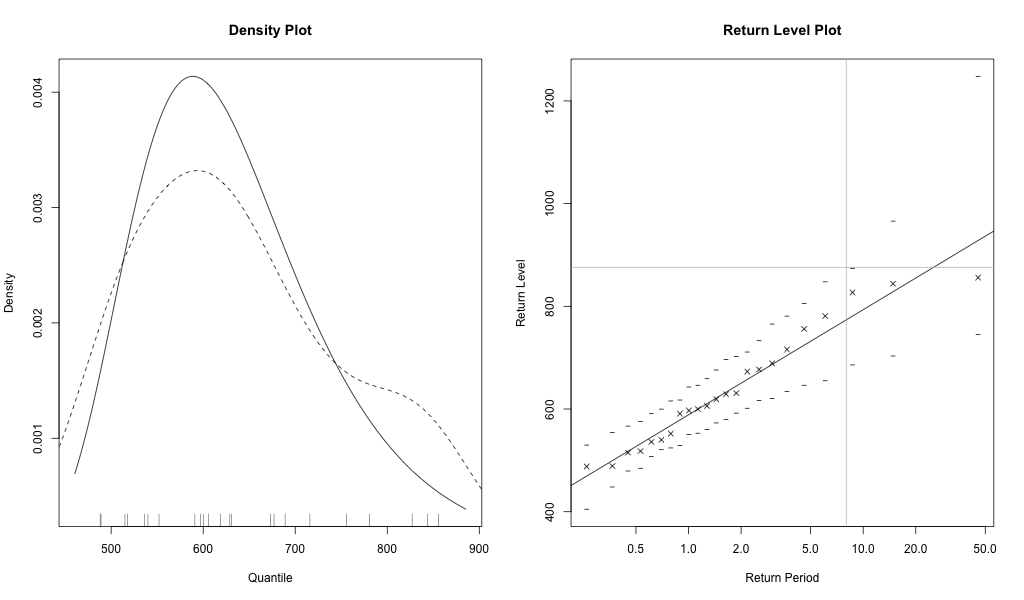
A mostani árvíz vízszintje esetében a visszatérési idő felső konfidencia intervalluma 8 év, ami azt jelenti, hogy akár 8 évenként is előfordulhat a mostanihoz hasonló nagyságú árvíz, és 10 évente akár 900 centiméteres árvízre is számíthatunk.
Az erre kijelölt szervek helyében én már most elkezdenék gondolkodni a jövőbeni védekezésen...
Az elemzést az R statisztikai programcsomag evd csomagját használtam.
Kmetty Zoltán
